Conocimientos previos necesarios:
Para consultar dudas sobre los temas clicka en los enlaces siguientes:
Para consultar dudas sobre los temas clicka en los enlaces siguientes:
Objetivo: Ayudar al estudiante de bachillerato a adquirir las competencias necesarias en el área de la geometría analítica.
Dirigido a: Alumnos de bachillerato cursando el tercer semestre o personas interesadas en la geometría analítica d nivel bachillerato.
A continuación describiremos los temas a tratar en la primera unidad explicando cada uno al final del índice de contenidos de la primera unidad.
Índice de contenidos temáticos
Primera unidad
La recta
1.- Geometría analítica
1.1.- Conceptos básicos
1.1.1.- Geometría analítica
1.1.2.- plano cartesiano
1.1.3.- Coordenadas de un punto
1.2.- Distancia entre dos puntos
1.2.1.- El punto medio
1.2.1.- El punto medio
1.3.- Pendiente de recta
1.4.- Obtención de la ecuación de la recta
1.4.1.- A partir de un punto y la pendiente
1.4.2.- A partir de dos puntos
1.4.3.- Tabulación y graficación
1.4.3.- Tabulación y graficación
1.5.- Paralelismo y perpendicularidad
1.6.- Distancia entre un punto y una recta
1.7.- Área de un polígono
Desarrollo de temas
Geometría analítica es el estudio de ciertos objetos geométricos mediante técnicas básicas del análisis matemático y delálgebra en un determinado sistema de coordenadas.
El plano cartesiano es un sistema de referencia respecto ya sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecto a tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas (o rectangulares) x e y se denominan abscisa y ordenada, respectivamente.
En la figura siguiente figura tenemos un plano cartesiano bidimensional en el cual se localizan 4 puntos.
A continuación tenemos una imagen de Rene Descartes quien es considerado el padre de la geometría analítica.
René Descartes1 (La Haye en Touraine;2 31 de marzo de 1596 – Estocolmo, 11 de febrero de1650) fue un filósofo, matemático y físico francés, considerado como el padre de la filosofía moderna, así como uno de los nombres más destacados de la revolución científica. Formuló el célebre cogito ergo sum, elemento esencial del racionalismo occidental. En física está considerado como el creador del mecanicismo, y en matemáticas, de la geometría analítica. No obstante parte de sus teorías han sido rebatidas - teoría del animal-máquina - o incluso abandonadas - teoría de los vórtices. Su pensamiento pudo aproximarse a la pintura de Poussin3por su estilo claro y ordenado.
El plano cartesiano se divide en cuatro cuadrantes y estos se numeran en contra sentido de las manecillas del reloj, siendo el primer cuadrante el de la derecha superior (cuadrante I), el segundo (cuadrante II), el tercero (cuadrante III) y el cuarto (cuadrante IV) a continuación una ilustración.
Coordenadas de un punto
Los puntos están expresados en letras mayúsculas y sus coordenadas se escriben en el siguiente orden: Punto A (x,y) es decir la primera cantidad representa las abscisas y la segunda a las ordenadas. y se ubican de la siguiente manera la primer cantidad se busca en la recta horizontal y la segunda en la recta vertical el punto se ubica en el cruce de ambas lineas como se aprecia en la imagen.
Distancia entre dos puntos
Para entender este tema debemos de aclarar que la distancia puede ser distancia horizontal, distancia vertical y distancia con pendiente. Primero explicaremos en una recta como se obtiene la distancia en una sola dimensión utilizando la recta numérica:
Formula: DH = (X2 -X1) si solo si X2 > X1
Respetando que: - a < 0 < a o sea cualquier cantidad negativa es menor que cero y cero es menor que cualquier cantidad positiva.
Por lo tanto X2 será 2 y X1 será -3 entonces la ecuación se expresa así:
DH = (X2 -X1) DH = [ 2 – (- 3) ] DH = ( 2 + 3 ) DH = 5
DH = distancia horizontal
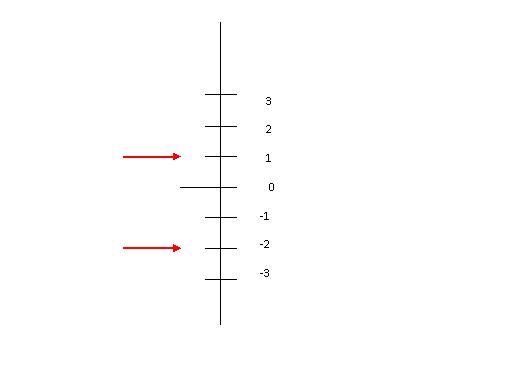
Y para el caso de la distancia vertical será:
Formula: DV = (Y2 -Y1) si solo si Y2 > Y1
ejemplo:
Por lo tanto Y2 será 1 y Y1 será -2 entonces la ecuación se expresa así:
DV = (Y2 -Y1) DV = [ 1 – (- 2) ] DV = ( 1 + 2 ) DV = 3
DV = distancia vertical
"Distancia con pendiente"
para el estudio de la distancia entre dos puntos haremos un comparativo entre la formula y el teorema de Pitágoras:
para identificar un segmento de recta se la designaran los puntos que lo formen ejemplo:
Formula para calcular la distancia entre dos puntos:
AB² = (X2 -X1)² + (Y2 -Y1)²
Teorema de Pitágoras:
h ² = a² + b²
Haciendo un comparativo:
Tenemos que: AB² = h² es la distancia con pendiente (inclinada)
(X2 -X1)² = a² es la distancia horizontal
(Y2 -Y1)² = b² es la distancia vertical
Identificando los puntos:
El punto "A" sera A (3,1); El punto "B" sera B (-1,-3); El punto "C" sera C (3,-3).
La distancia que calcularemos sera la "AB" para ello elegiremos el punto mayor
el cual sera el que tenga la "Y" mayor en este caso sera el punto "A" al cual consideraremos como A ( X2, Y2 ) y B (X1 -Y1) entonces sustituyendo en la formula:
AB² = (X2 -X1)² + (Y2 -Y1)²
AB² = (3 -(-1))² + (1 -(-3))²
AB² = (3 +1)² + (1 +3)²
AB² = (4)² + (4)²
AB² = 16 + 16
AB² = 32
AB = 5.65
"El punto medio"
Es la mitad de la distancia entre dos puntos y esto se calcula de la siguiente manera:
X = (X2 + X1) / 2 y Y = (Y2 + Y1) / 2
Aplicando esto en el ejercicio anterior seria:
X = (3 + (-1)) / 2 y Y = (1 + (-3)) / 2
lo cual nos deja:
X = (3 - 1) / 2 y Y = (1 - 3) / 2
X = 2 / 2 y Y = - 2 / 2
X = 1 y Y = - 1
por lo tanto el punto medio seria:
Punto medio M (1,-1)
"Pendiente de recta"
La pendiente de una recta es la inclinación que esta presenta es decir el angulo que forma con referencia al eje "X" y esta pendiente esta expresada como una tangente el angulo se toma en contra del sentido de las manecillas del reloj y su formula es así:
m = (Y2 -Y1) / (X2 -X1)
sustituyendo por los valores del ejercicio anterior:
Identificando los puntos:
El punto "A" sera A (3,1); El punto "B" sera B (-1,-3), elegiremos el punto mayor el cual sera el que tenga la "Y" mayor en este caso sera el punto "A" al cual consideraremos como A ( X2, Y2 ) y B (X1 -Y1), muy importante cuidar este detalle ya que sino lo hacemos tendremos una pendiente invertida ya que no seria lo mismo "a" que "-a" por que pendientes negativas dan ángulos negativos.
sustituyendo por los valores del ejercicio anterior:
m = (1 -(-3)) / (3 -(-1)) entonces: m = (1 + 3) / (3 + 1) por lo tanto:
m = 4 / 4 y resulta: m = 1
y esta resultado recordemos es una tangente por lo tanto si le damos inversa tangente:
m = 1 es 45 grados
"Obtención de la ecuación de una recta"
La ecuación de una recta se obtiene a partir de su pendiente y de un punto básicamente es como casi todo problema matemático que tan solo se requieren dos datos para resolverse aunque para su estudio lo dividimos en dos casos:
a) A partir de un punto y la pendiente
b) A partir de dos puntos
Aunque al final es lo mismo ya que con dos puntos calculamos la pendiente y con la misma y un punto obtenemos la ecuación hagamos un ejercicio del primer caso:
Tenemos que: m = 4/5 y el punto A(0,4)
Recordemos utilizaremos la formula de la pendiente solo que despejada:
m = (Y2 -Y1) / (X2 -X1) despejando Y2 -Y1 = m (X2 -X1)
Recordemos que siempre sustituiremos por el punto menor en este caso (X1 -Y1) tomara los valores del punto P(0,4).
sustituyendo Y - 4 = 4/5 ( X - 0 )
Y - 4 = 4/5X
Aquí en este punto podemos despejar cualquiera de las variables o expresarla como ecuación general de primer grado con dos variable recapitulando:
AX + BY + C = 0 por lo tanto:
- 4/5X + Y - 4 = 0
recordemos que la podemos expresar en enteros aplicando la propiedad de la uniformidad:
(- 4/5X + Y - 4 = 0) (5) obtenemos:
- 4X + 5Y - 20 = 0
y aun podemos arreglarla para que "X" sea positiva aplicando la misma propiedad:
(- 4X + 5Y - 20 = 0) (- 1) resultando:
4X - 5Y +20 = 0
Ejemplo gráfico
Bien a partir de la ecuación general obtendremos la ecuación despejada de la variable "Y" así:
4X - 5Y +20 = 0 despejando "Y":
- 5Y = - 4X - 20
Y = (- 4X - 20) / - 5
Y = - 4X / - 5 - 20 / - 5
Y = 4 / 5X + 4
Entonces para el segundo caso se calcularía primero la pendiente y después se tomaría uno de los puntos y se realizaría el mismo procedimiento.
"Tabulación y graficación"
Expliquemos lo tabular significa es a partir de la ecuación despejada se le dan valores a una de las variables y se van sustituyendo en la ecuación para ir obteniendo los valores de la variable dependiente y estos se van registrando en una tabla de valores.
Tenemos la ecuación: Y = 2X - 4
Demos valores arbitrarios a la variable independiente (en este caso "X") y estos serán de -2 hasta 2 o sea:
-2,-1,0,1,2
La tabla quedaría así:
Procedamos a obtener los valores de la variable dependiente (en este caso "Y") Tenemos la ecuación: Y = 2X - 4
Demos valores arbitrarios a la variable independiente (en este caso "X") y estos serán de -2 hasta 2 o sea:
-2,-1,0,1,2
La tabla quedaría así:
tenemos las ecuación:
Y = 2X - 4 sustituyendo por los valores de la tabla:
Y = 2(-2) - 4 Y = 2(-1) - 4 Y = 2(0) - 4 Y = 2(1) - 4 Y = 2(2) - 4
Y = - 4 - 4 Y = - 2 - 4 Y = 0 - 4 Y = 2 - 4 Y = 4 - 4
Y = - 8 Y = - 6 Y = - 4 Y = - 2 Y = 0
La tabla quedaría así:
"Graficando"
Daremos nombres a los puntos A(2,0); B(1,-2); C(0,-4); D(-1,-6) y E(-2,-8) la gráfica quedaría así:
"Paralelismo y perpendicularidad"
Recordemos lo que son rectas paralelas y lo que son rectas perpendiculares para entrar al estudio de estas condiciones en la geometría analítica:
Rectas paralelas:
Son aquellas que equidistan en todos sus puntos (mantienen la misma distancia nunca se acercan ni alejan en todo lo largo).
En geometría analítica la condición que debe tener una recta para ser paralela a otra es que sus pendientes sean iguales.
La recta AB es paralela a la recta CD si y solo si mAB es igual a la mcd
la ecuación queda así: mAB = mcd
En este ejemplo vemos que ambas pendientes son 0.67 por lo tanto son rectas paralelas para ello pasaremos a la demostración matemática:
A(2,6); B(-4,2) forman la recta AB C(2,-7); D(8,-3) forman la recta CD
calculemos ambas pendientes para comprobar si son paralelas y nos deben dar pendientes iguales:
m = (Y2 -Y1) / (X2 -X1) m = (Y2 -Y1) / (X2 -X1)
m = (6 -2) / (2 -(-4)) m = (-3 -(-7)) / (8 -2)
m = (4) / (2 +4 ) m = (-3 + 7) / (6)
m = 4 / 6 m = 4 / 6
Son iguales por la tanto las rectas son paralelas
Rectas paralelas:
Son aquellas que equidistan en todos sus puntos (mantienen la misma distancia nunca se acercan ni alejan en todo lo largo).
En geometría analítica la condición que debe tener una recta para ser paralela a otra es que sus pendientes sean iguales.
La recta AB es paralela a la recta CD si y solo si mAB es igual a la mcd
la ecuación queda así: mAB = mcd
En este ejemplo vemos que ambas pendientes son 0.67 por lo tanto son rectas paralelas para ello pasaremos a la demostración matemática:
A(2,6); B(-4,2) forman la recta AB C(2,-7); D(8,-3) forman la recta CD
calculemos ambas pendientes para comprobar si son paralelas y nos deben dar pendientes iguales:
m = (Y2 -Y1) / (X2 -X1) m = (Y2 -Y1) / (X2 -X1)
m = (6 -2) / (2 -(-4)) m = (-3 -(-7)) / (8 -2)
m = (4) / (2 +4 ) m = (-3 + 7) / (6)
Son iguales por la tanto las rectas son paralelas
Recordemos dos rectas son perpendiculares cuando se intersectan y forman ángulos rectos.
Bien ahora para que una recta sea perpendicular a otra sus pendientes al ser multiplicadas tendrán un producto igual a -1.
Es decir:
mAB mcd = -1
En el ejercicio anterior la pendiente mAB= -2.50 y mcd =0.40 entonces tenemos que:
(-2.50) (0.40) = -1 por lo tanto las rectas son perpendiculares
3X + 4Y - 21 = 0 comparando: AX +BY + C = 0
sustituyendo en la formula tomando en cuenta que P(1,2):
d = (3(1) + 4(2) - 21) / (9 + 16)**1/2
d = ( 3 + 8 - 21) / (25)**1/2
d = -10 / 5
d = - 2
La distancia dirigida es positiva cuando el punto se encuentra por encima de la recta y es negativa cuando esta por debajo.
como podemos apreciar en este ejemplo la distancia resulto ser negativa por estar el punto por debajo de la recta.
Para llevar a buen desarrollo esta tema debemos de recordar lo que son las determinantes y la regla de sarrus
Es decir:
mAB mcd = -1
En el ejercicio anterior la pendiente mAB= -2.50 y mcd =0.40 entonces tenemos que:
(-2.50) (0.40) = -1 por lo tanto las rectas son perpendiculares
"Distancia entre un punto y una recta"
Esto es lo que conocemos como "distancia dirigida" y se calcula con la siguiente formula:
Aplicando esta formula a un ejemplo veremos como se desarrolla a continuación tenemos el ejemplo gráfico:
Tenemos que la ecuación es:
Y = (- 3X + 21) / 4
cambiándola a su forma general lo cual seria:
3X + 4Y - 21 = 0 comparando: AX +BY + C = 0
sustituyendo en la formula tomando en cuenta que P(1,2):
d = (3(1) + 4(2) - 21) / (9 + 16)**1/2
d = ( 3 + 8 - 21) / (25)**1/2
d = -10 / 5
d = - 2
La distancia dirigida es positiva cuando el punto se encuentra por encima de la recta y es negativa cuando esta por debajo.
como podemos apreciar en este ejemplo la distancia resulto ser negativa por estar el punto por debajo de la recta.
"El área de un polígono"
Para llevar a buen desarrollo esta tema debemos de recordar lo que son las determinantes y la regla de sarrus